Resistors
By Tim Surtell
|
|
 |
A resistor placed in a circuit will resist the passage of electrical current through it and will therefore alter the voltages in the circuit according to Ohm's Law...
![]()
...which relates voltage (V in Volts) to current (I in Amps) and resistance (R in Ohms). The unit 'Ohms' has its own symbol, the Greek capital letter Omega (Ω).
If you need to find out the current flowing through a resistor, or the resistance of a resistor, you can easily re-arrange Ohm's Law to find these quantities...
![]()
Resistor values that are available for use in circuits range from 0Ω to around 10,000,000Ω. Because dealing with large numbers like 10,000,000 is awkward, the 'k' prefix is used to denote 1,000 and the 'M' prefix is used to denote 1,000,000. 'k' stands for 'kilo' and 'M' stands for mega. Here are some examples of resistor values:
1kΩ = 1,000Ω (pronounced 'one kilo Ohm' or 'one k' for short)
10MΩ = 10,000,000Ω (pronounced 'ten mega Ohms' or 'ten meg' for short)
Sometimes you will see resistors quoted without the Ω symbol, and sometimes the symbol will be replaced with 'R'. When a fraction is needed in a value you will often see 'R', 'k', or 'M' in place of the decimal point as an aid to clarity:
22k is the same as 22kΩ
330R is the same as 330Ω
4K7 is the same as 4.7kΩ
Rather than using resistors of every conceivable value, circuit designers tend to stick to two series of values that will include values close enough to the value they have calculated. You will see these resistors for sale in electronics catalogues and you will notice the patterns in the series.
When the value of a particular resistor is not that important in a circuit, you will also often see the 'standard' values of 1kΩ and 10kΩ being specified - it is therefore a good idea to keep a good stock of these in your components box!
If you do need a resistor of exact value, but you don't have one, you could always combine two or more resistors to get the correct value. This is done by placing the resistors in 'series' or 'parallel' as shown in figure 1.
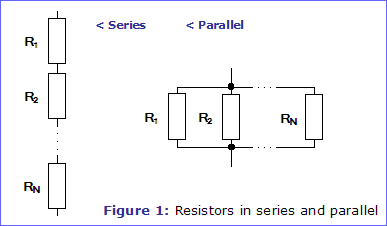
If you place resistors in series, the total value of the combination is the value of each resistor added together. For example, a 10kΩ resistor in series with another 10kΩ resistor makes a total of 20kΩ.
Placing resistors in parallel is slightly more complicated, since the total value of the combination will be the result of the following formula...
![[Equation] [Equation]](equations/014_03.gif)
...where Rtotal is the total combination, and R1 to Rn are the values of each resistor in the combination.
If both resistors in the combination are of the same value, it is easy - the total value of the combination is half the value of one of the resistors. For example, a 10kΩ resistor in parallel with another 10kΩ resistor makes a total of 5kΩ.
Like all components, resistors are never perfect. Their true value will never be exactly the same as their stated value, but will be somewhere close. The maximum amount of error in the value is given by the 'tolerance' value, expressed as a percentage. Most resistors have a 10% - 20% tolerance, and this is normally adequate for most applications. You can get 1% and 2% tolerance resistors if you need them.
Resistors also have a power rating, expressed in Watts (W), which needs to be taken into account when choosing the type of resistor needed in a circuit. For most low voltage, low current circuits like those in Electronics in Meccano, 0.6W resistors will be adequate. Where a higher rating is required, it will be stated.
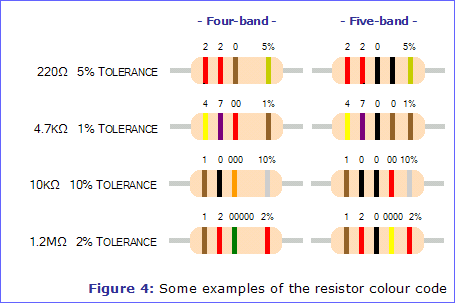
Because resistors are so small, it is not easy to print their value and tolerance on them in a way which is easily readable. Therefore, one of the following colour coding systems is used instead. Both systems code the value in Ohms - there are no codes for 'k' or 'M'.
This system uses three coloured bands to represent a resistor's value, and an additional coloured band spaced further apart to represent a resistor's tolerance, as shown in figure 2.
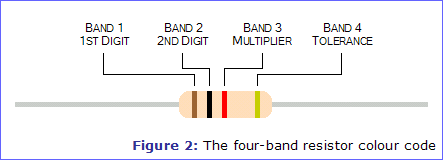
The table below shows the meaning of each colour for each of the bands. Notice that most of the colours are in the order of the colours of a rainbow, with the exception of indigo which is not used. There is a rhyme you can use to remember these colours: Richard Of York Gave Battle in Vain.
| Colour | Band 1 1st Digit |
Band 2 2nd Digit |
Band 3 Multiplier |
Band 4 Tolerance |
||||
| Black | 0 | 0 | x 1 | - | ||||
| Brown | 1 | 1 | x 10 | 1% | ||||
| Red | 2 | 2 | x 100 | 2% | ||||
| Orange | 3 | 3 | x 1,000 | - | ||||
| Yellow | 4 | 4 | x 10,000 | - | ||||
| Green | 5 | 5 | x 100,000 | - | ||||
| Blue | 6 | 6 | x 1,000,000 | - | ||||
| Violet | 7 | 7 | - | - | ||||
| Grey | 8 | 8 | - | - | ||||
| White | 9 | 9 | - | - | ||||
| Gold | - | - | - | 5% | ||||
| Silver | - | - | - | 10% | ||||
The five-band system uses the same colours as the four band system, but uses them slightly differently. An extra band is included which acts as another digit, and the colours Gold and Silver are used as additional multipliers of 0.1 and 0.01. The five-band system can therefore represent values to three significant figures and also values lower than 1Ω.
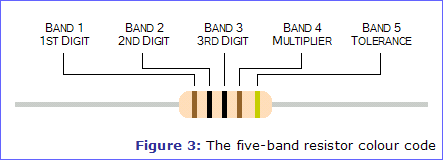
The table below shows the meaning of each colour for each of the bands.
| Colour | Band 1 1st Digit |
Band 2 2nd Digit |
Band 3 3nd Digit |
Band 4 Multiplier |
Band 5 Tolerance |
|||||
| Silver | - | - | - | x 0.01 | 10% | |||||
| Gold | - | - | - | x 0.1 | 5% | |||||
| Black | 0 | 0 | 0 | x 1 | - | |||||
| Brown | 1 | 1 | 1 | x 10 | 1% | |||||
| Red | 2 | 2 | 2 | x 100 | 2% | |||||
| Orange | 3 | 3 | 3 | x 1,000 | - | |||||
| Yellow | 4 | 4 | 4 | x 10,000 | - | |||||
| Green | 5 | 5 | 5 | x 100,000 | - | |||||
| Blue | 6 | 6 | 6 | x 1,000,000 | - | |||||
| Violet | 7 | 7 | 7 | - | - | |||||
| Grey | 8 | 8 | 8 | - | - | |||||
| White | 9 | 9 | 9 | - | - | |||||
Figure 4 shows a few examples of the resistor colour code using both systems.
Most resistors look like the ones shown below left, although their thickness will increase as their power rating increases. Surface mounting resistors like those shown below right are also available, but since they are so small and hard to handle and solder, they won't be of much use to the hobbyist.


Resistors normally come on a bandolier - two strips of paper like the ones shown above left. The resistors are spaced 5mm apart so that they can be easily fed into machines that bend and cut the leads automatically. Unless you have access to such a machine, you will need to do this yourself in order to mount your resistors onto a PCB or piece of stripboard. First, bend one of the leads to 90° using pliers, then use an off-cut of stripboard to get the bend in the other lead in exactly the right place.
Resistors can be placed either way round and they are not damaged by the heat of soldering.
| |
  |
In many circuits the value of a resistor needs to be adjusted by the user when the circuit is in use. One easy way to achieve this is to replace the resistor with a variable resistor. Variable resistors have a shaft which, when turned, will increase their resistance smoothly from around 0Ω up to their marked resistance value.
The shaft is connected to a 'wiper' inside the variable resistor which makes contact with a circular track made of a resistance material, which will be laid out in either a 'linear' or 'logarithmic' fashion. Most circuits will use variable resistors with a linear track (usually marked 'LIN'), although you will find logarithmic variable resistors (usually marked 'LOG') used as volume controls, for example in audio amplifier circuits.
Most variable resistors are designed to be turned easily by hand, and come with long shafts that can be trimmed to length for panel mounting. The end of the shaft can be fitted with one of many styles of control knob.
Almost all variable resistors that you can buy have three terminals; one connected to each end of the track and one (usually the centre) connected to the wiper. These variable resistors are called 'potentiometers' and have a different circuit symbol to those that have only two terminals, which are called 'rheostats'.
Sometimes a resistance in a circuit will only need to be adjusted once, perhaps to calibrate a circuit, and it will rarely be adjusted again. In this situation, small 'preset' variable resistors can be used. These are normally adjusted using a small screwdriver so that the shaft position cannot be altered by accident.



Article Information
Source: Electronics in Meccano - www.eleinmec.com
| First published in EiM: Issue 1 (September 1998)
Topic: Components Explained |
Created: 16/05/2002 |
Last modified: 13/02/2007
Top of Page | Homepage | About | Search | Topics | Features | Circuits Shop | yourEiM |
© 1998 - 2024 Tim Surtell |